Rifling and gravitational effects

THE TWIST OF RIFLING, DRIFT, YAW AND THE ROTATION OF THE EARTH

Taken from the British "Text Book of Small Arms - 1929" pages 288 to 292

In 1879 Bashforth's successor at Woolwich, Professor Greenhill, found that the sharp spin given to howitzers set up such heavy torsional strains between the liner of the gun and the jacket that the gun sometimes wrung its own neck, and by shearing the copper vent automatically spiked itself. The spin was usually cut at one turn in 12 calibres, so that a 6-inch howitzer shell turned round once in each six feet advance (or one in 12 calibres), equivalent to 1 turn in 31 inches for the • 303 rifle. Thereupon he set himself to investigate the whole question of the spin of rifling required to produce steady flight against the resistance of the air, a subject which was then in a chaotic state. The mathematical argument was exceedingly complicated, but it resulted in a simple table of the minimum spin that is required to overcome instability.

As pointed out at the time by Captain J. P. Cundill, the hypotheses underlying the table are as follows :---

(a) The projectile is of the form of a prolate spheroid, or egg-shaped, the only shape for which the " stream-lines " are known.
(b) The medium through which it moves is frictionless and homogeneous (i.e., incompressible).
(c) Gravity is neglected, and hence the curvature of the trajectory does not enter into the problem.

The validity of these assumptions has been a matter of considerable controversy, as they are obviously unsatisfied by any bullet flying in air ; but it is found that in the case of rifle bullets a reduction of spin in the proportion of 4 to 3 below the tabular value is a sufficient and reliable discount for the hypotheses, and gives enough and not too much spin for stability. The table can be obtained for all practical purposes from the following rule for solid lead bullets of specific gravity 0.9. "The length of the bullet in calibres multiplied by the spin required in calibres is 150."

Thus for a bullet 5 calibres long (or 1¹/2 inches for • 303) the greatest twist required is one turn in 30 calibres or 1 turn in 9 inches for • 303. When the density of the bullet is less than that of lead or the density of the resisting medium is greater than that of air, the spin should be increased as the square root of the ratio of the densities. Thus aluminium is four times as light as lead and requires double the spin, whereas water is 900 times as heavy as air so that the spin has to be increased 30-fold if the bullet is to be stable in water. Hollow shell such as the cupro-nickel envelope of a Mark VII bullet from which the lead has been melted require rather more spin than solid bullets, but so little more that the • 303 rifle will fire an empty envelope correctly. The actual calibre of the bullet is of no consequence, as the rule is expressed in calibres ; nor is the actual muzzle velocity, because the number of turns per second varies as the muzzle velocity.
In the steady or stable motion of a bullet the centre of gravity describes a very long helix of very small diameter ; in fact, the bullet must always be a slight " tipper " ; but the tipping is very small indeed, as the length of the helix of the • 303 is about 5 yards and its diameter less than one-hundredth of an inch. In actual practice Greenhill's figure 150 can be increased safely to 200 and still control the bullet. This reduction of spin required in practice is probably due to air being compressible, viscous, and possessed of friction.

In a later unpublished paper written in 1912 Sir George Greenhill investigated the stability of the shot whilst it was passing up the barrel. He pointed out that centrifugal wringing machines used in steam laundries or milk separators were driven either from above or below according to the weight and speed employed. The central spinning shaft for a slow moving centrifugal can well be taken from the roof with the centrifugal hanging from it, but if any fast spinning is required a roof suspension will smash itself to pieces, necessitating the shaft coming up through the floor for high speeds. The centrifugal pan then rides and spins quietly like a top asleep, which it really is. So, too, a shot as it starts slowly from the breech should be rotated by a driving band slightly in front of the centre of gravity, but as speed is picked up the rotating band should be moved (if such a thing were possible) to some position one or two calibres behind the centre of gravity if the shot is not to " fight " on its way to the muzzle and damage itself and the gun. With rifle bullets the rotating ring is really the whole of the parallel of the bullet and the fighting power of the bullet is so controlled by the enormous surface of contact that it has little chance to display itself. From the most recent experiments with stream-line bullets, which have a much shorter bearing surface, it seems probable that more attention will have to be given to this subject than in the past.
As a direct result of the spinning of the bullet in the air the phenomenon of " drift " is observed.

It was in 1746 that Benjamin Robins showed that the sole virtue of rifling lay in giving spin to the ball on a predetermined axis. No ball could be fired from a smooth bore without rubbing against the sides of the bore and acquiring a spin, the axis of which depended on the chance position of the last rubbing contact. He relates that he purposely bent a musket barrel a few degrees to the left 3 or 4 inches from the muzzle, and predicted that the bullet would incurvate to the right, and " this upon trial did most remarkably happen."

The following explanation of the effect of rifling and the phenomenon of drift, together with the plates, is reproduced from the Text-book of Gunnery, 1887, by Major G. Mackinlay, pages 133 and 242 :-
" Let us consider why a rifled projectile, which rotates about its longer axis, can be made to travel through the air with its point always approximately first. Suppose that the projectile has reached some position, D (Fig. 5), in its flight, where gravity has caused the axis to make a certain angle with the trajectory ; we may suppose the resultant resistance of the air to act along SR. But the effect of the couple R.GM in the case of a spinning shot, is not to raise the point of the projectile and give rotation round the centre of gravity, on an axis at right angles to the plane of the trajectory ; but it causes a slow movement of the point laterally, with service projectiles having right-handed rotation, to the right of an observer stationed behind the gun and who looks down the range ; with left-handed rotation the movement would be to the left. This is shown in the plan, and the projectile sets laterally across the original direction. As seen in the plan, the couple R.GM, instead of turning the point still more to the right, gives it a slow downward movement. The point is thus approximately kept down to the trajectory. The resultant resistance, as seen in the plan, also exercises a retarding effect, and as the direction of the projectile is inclined to this resultant, a lateral force is exerted, which causes a tolerably uniform lateral acceleration, giving rise to drift to the right. The plan of the trajectory is thus seen to be a curved line and not a straight one, and the trajectory itself has a double curvature, and is not contained in one plane.
" The gyroscope illustrates the stability of the direction of the axis of a spinning body and the tendency of a rifled elongated projectile to travel nearly point first in flight, and it also gives a reason for the slight turning movement of the axis of the projectile caused by the resistance of the air.
" A gyroscope (Fig. 6) for such a purpose consists of a carefully centred heavy model of an elongated projectile, some 2¹/2 inches long, free to revolve on pivots inside a brass ring, the axis of revolution being a diameter of the ring, which has externally two arms in its

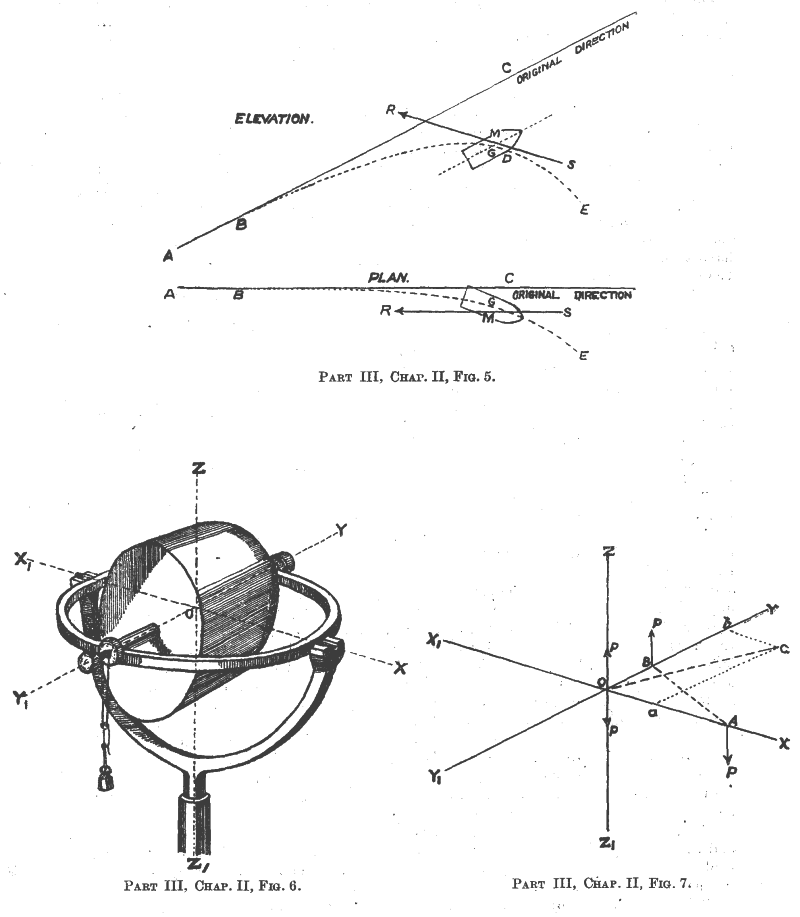
own plane, in prolongation of a diameter at right angles to the axis of the projectile. On these the ring can revolve in bearings in a vertical brass hall ring, which has a stem under its middle fitting into a socket in a heavy stand. The half ring can revolve round its vertical axis.
" The centre of gravity of the model projectile is adjusted to be over the vertical stem by screwing the bearings of the pivots in or out together, and it will then remain in any position. All the three axes of rotation intersect in the centre of gravity 0 of the projectile,. and movement of the axis in any direction is easy.
" If the gyroscope's projectile (not spun) is placed horizontally as in the figure, and a small weight is suspended from the brass ring behind it, the point of the projectile will immediately rise ; and thus the effect of the couple caused by the resistance of the air in raising the point of a non-rotating elongated projectile in flight is imitated. But if the model projectile is caused to spin round its longer axis with a right-handed rotation, the addition of a small weight causes the axis to move its point round to the right (looking from behind it) with a slow movement in a horizontal plane, and thus the couple caused by the resistance of the air on a rotating projectile in flight is imitated. If one of the bearings on the brass ring is now pushed laterally in the direction of this motion, it does not increase the movement, but the axis turns in a plane at right angles and the point dips.

" In these last two cases a turning motion of the axis ensues in a plane at right angles to the couple, similar to the lateral movement of the axis of an elongated projectile in flight.
" This can be explained as follows :-
" Place the brass ring horizontal, and through 0, the centre of gravity of the model projectile (Fig. 6), draw the three axes of revolution at right angles to each other, and call them OX, OY, OZ. Reproduce these lines in Fig. 7, which (for simplicity) is divested of the rings, projectile, etc., of Fig. 6. The original rotation round the axis Y Y₁ (Fig. 7), may be represented by a couple P.OA ; with a certain length of arm OA : the couple caused by the weight, or by the resistance of the air in the case of a real projectile in flight, may be shown by P.BO, the force P being taken equal in both couples, but the arms different in length, since the couples are not equal to each other. Mark off on OY a distance Ob OA, on OX make Oa OB, and complete the parallelogram ab' with its diagonal Oc. The forces P and P at 0 neutralize each other as they are equal, and act along the same line in opposite directions, and there remain P at B, and P at A, constituting only one couple, causing rotation about a fresh axis Oc, which is the diagonal of the parallelogram ab, and at right angles to AB. This indicates that the axis of revolution slowly moves from the direction Y₁ Y to Oc ; and this turning movement will continue as long as both couples exist.

" The very slow continuous change of the inclination of the earth's axis, called the precession of the equinoxes, is a movement of a similar nature, which can also be illustrated by means of the gyroscope."

The actual amount of drift at ranges up to 1,100 yards with the • 303 Mark VII is known by actual trial on a large and careful scale to be less than one foot or one minute of angle. This is easily proved by setting the sights to the correct elevation and deflection to make central bull's-eyes at 1,000 yards in a flat calm. Aim is taken at a small bull on a large card at 25 yards. The shot holes are then found about 14 inches above the bull and less than ¹/4 inch to the right of the plumb-line through the bull.
At ranges up to about one mile, as pointed out by Metford, an inclination of the back sight to the right of about two degrees for a left-hand spiral corrects very well for the effect of drift. At ranges greater than about a mile the drift is more considerable, and may amount to as much as 100 yards at extreme ranges. A good working rule, then, is to multiply the tangent elevation in degrees by four and allow that number of minutes right deflection to correct for drift.

" Yaw " is a phenomenon observed more or less with all guns at long ranges.

Firing over large stretches of sea-sand, the bullets make holes or marks in the sands which clearly indicate that they are not flying with their spinning axis parallel to the tangent of the trajectory. Divergences of as much as 45 degrees are by no means uncommon. The actual efficient cause of yaw is not completely known, and is not simple. It is certainly gyroscopic in nature, and it increases distinctly with the rate of bending of the trajectory measured in degrees turn per second. In the first few hundred yards this rate is about one degree per second, but a little after the vertex of the 10-degree trajectory the rate has increased to seven degrees per second. At the same time, the forward velocity of the shot has fallen to about a quarter of its original value, and the rate of spin of the bullet has fallen very much less. This results in the bullet having a very great amount of over-spin just at the time when the bullet requires to turn its nose down quickly so as to keep parallel with the trajectory.
The rate of diminution of spin is not known. The Mark VII starts with the prodigious spin of one-sixth of a million revolutions per minute, or 2,930 revolutions per second, and perhaps loses its spin at the rate of 5 or 10 per cent. per second. If it lost its spin at the rate of 10 per cent. per second, it would still be spinning at 1,380 r.p.s. after seven seconds, and at 2,000 r.p.s. if the loss was only 8 per cent. per second. If the loss was as low as 3¹/2 per cent. per second it would be spinning at 10 r.p.s. after 1,000 seconds, or rather over a quarter of an hour. The effect of yaw is to increase the air resistance enormously and to shorten the range.
The rotation of the earth during the time of flight of a bullet has a real effect on both its range and its direction, although these are both extremely small. In very powerful naval guns at very long ranges a correction may properly be made for its effect. Metford pointed out that a bullet in its flight behaves like Foucault's pendulum, so that if at the instant of firing the plane of the trajectory passes through a particular star near the horizon, it continues to pass through that star throughout its flight. The star moves 360 degrees in 24 hours, or a quarter of a minute of angle in one second of time. In a vacuum the effect may be considerable, but in actual air it may be neglected in comparison with other causes of error. Cranz works out numerically an example of a 12-inch gun with velocity 2,500 f/s fired due north in latitude 54 N. and at an angle of elevation of 40 degrees, giving a range of 37,000 yards. The effect is to shorten the range by 10 yards with 160 yards right deviation.

Return to: TOP of PAGE

See this website's Raison d'être